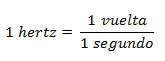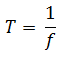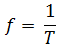FÍSICA 3ERO BACH

Oscilador Armónico Simple

La fuerza que produce un M.A.S es una fuerza central dirigida hacia el punto de equilibrio y proporcional a la distancia a éste.

El período de un oscilador sometido a una fuerza elástica depende de su constante recuperadora y de su masa, pero no depende de la amplitud del movimiento.

El período de oscilación es:

T=2\pi {\sqrt {m \over k}}

Péndulo Simple

El movimiento del péndulo simple es un movimiento armónico simple siempre que se consideren desplazamientos muy pequeños.

T=2\pi {\sqrt {m \over k}}

tendríamos:

(12) $F=-k\,x=m\,a\qquad \Rightarrow \qquad a=-{\frac {k}{m}}x$

Comparando esta ecuación y la que teníamos para la aceleración se deduce:

(13) $\omega ^{2}={\frac {k}{m}}$

Resultado de imagen para grafica pendulo simple

Actividad: Resolver la actividad de la página 63 del texto del ministerio.

GRÁFICA DEL M.A.S
Una partícula posee un movimiento armónico simple a lo largo de un eje X cuando su elongación x, o coordenada de posición sobre este eje, se expresa mediante una función sinusoidal del tiempo dado.

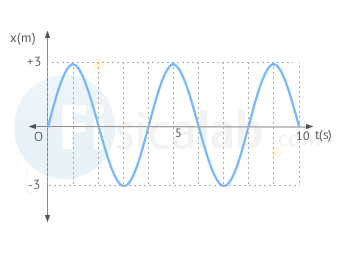Resultado de imagen

PERÍODO Y FRECUENCIA DEL M.A.S

El período T del M.A.S es independiente de la amplitud y su fórmula es:

T= período ; f= frecuencia ; w= velocidad angular

Frecuencia

La frecuencia mide la cantidad de vueltas que se dan en un período de tiempo (normalmente un segundo). Se calcula con la siguiente fórmula:

La unidad más utilizada es el hertz que equivale a una vuelta en un segundo.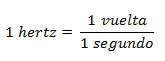

Período

El período mide el tiempo que se tarde en dar una vuelta completa y se mide en segundos. Es la inversa de la frecuencia.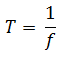

T = Período [s]
f = Frecuencia [Hz]

De esta forma, la frecuencia se puede calcular como la inversa del período.

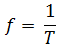f = Frecuencia [Hz]
T = Período [s]

Posición

La posición de una partícula que sigue un movimiento armónico simple ( m.a.s.), también denominada elongación, viene determinada por la distancia x a la posición de equilibrio. Su unidad de medida en el Sistema Internacional es el metro (m). Se trata de una función sinusoidal (seno o coseno), que depende del tiempo x = f(t).

Ecuación de posición

	x → Seno	x → Coseno
Con ω	$x = A \cdot sin (ω \cdot t + φ 0)$	$x = A \cdot cos (ω \cdot t + φ' 0)$
Con f	$x = A \cdot sin (2 \cdot π \cdot f \cdot t + φ 0)$	$x = A \cdot cos (2 \cdot π \cdot f \cdot t + φ' 0)$
Con T	$x = A \cdot sin (2 \cdot π T \cdot t + φ 0)$	$x = A \cdot cos (2 \cdot π T \cdot t + φ' 0)$

Donde:

A: Amplitud máxima del movimiento. Representa la distancia máxima a la posición de equilibrio. Su unidad de medida en el Sistema Internacional es el metro (m)
f: Frecuencia del movimiento. Es el número de oscilaciones o vibraciones que se producen en un segundo. Su unidad de medida en el Sistema Internacional es el Hertzio (Hz). 1 Hz = 1 oscilación / segundo = 1 s-1.
T: Periodo del movimiento. El tiempo que tarda en cumplirse una oscilación completa. Es la inversa de la frecuencia T = 1/f . Su unidad de medida en el Sistema Internacional es el segundo (s).
ω : Frecuencia angular o pulsación. Representa el número de periodos comprendidos en 2·π segundos. Su unidad de medida en el sistema internacional es el radián por segundo ( rad/s ). Se encuentra relacionada con la frecuencia y el periodo del movimiento según ω=2⋅πT=2⋅π⋅f
φ0 y φ'0 : Fase inicial. Se trata del ángulo que representa el estado inicial de vibración, es decir, la posición x del cuerpo en el instante t = 0. Su valor depende de si has elegido un seno o un coseno para representar el movimiento. φ'0=φ0−π/2 Su unidad de medida en el Sistema Internacional es el radián (rad) .

Para cualquier instante t se cumple que x(t)=x(t+T) .

Gráfica de posición x - t

Velocidad

La velocidad instantánea determina la variación de posición que tiene el cuerpo en cada instante de tiempo t. Se define como la derivada de la posición respecto al tiempo.

v = d x d t

Para obtener la expresión de la velocidad hemos de tener en cuenta que dependerá de si expresamos la posición como seno o como coseno:

v=ddt(A⋅sin(ω⋅t+φ0))=A⋅ω⋅cos(ω⋅t+φ0)
v=ddt(A⋅cos(ω⋅t+φ'0))=−A⋅ω⋅sin(ω⋅t+φ'0)

Ecuación de velocidad

	Velocidad (cuando x → Seno )	Velocidad (cuando x → Coseno )
Con ω	$v = A \cdot ω \cdot cos (ω \cdot t + φ 0)$	v=−A⋅ω⋅sin(ω⋅t+φ'0)
Con f	$v = A \cdot 2 \cdot π \cdot f \cdot cos (2 \cdot π \cdot f \cdot t + φ 0)$	$v = - A \cdot 2 \cdot π \cdot f \cdot sin (2 \cdot π \cdot f \cdot t + φ' 0)$
Con T	$v = A \cdot 2 \cdot π T \cdot cos (2 \cdot π T \cdot t + φ 0)$	$v = - A \cdot 2 \cdot π T \cdot sin (2 \cdot π T \cdot t + φ' 0)$

Para cualquier instante t se cumple que v(t)=v(t+T) .

Gráfica de velocidad v - t

Aceleración

La aceleración instantánea determina la variación de velocidad que tiene el cuerpo en cada instante de tiempo t. Se define como la derivada de la velocidad respecto al tiempo.

a = d v d t

Para obtener la expresión de la aceleración hemos de tener en cuenta que dependerá de si expresamos la posición como seno o como coseno:

a=d2dt2(A⋅sin(ω⋅t+φ0))=ddt(A⋅ω⋅cos(ω⋅t+φ0))=−A⋅ω2⋅sin(ω⋅t+φ0)
a=d2dt2(A⋅cos(ω⋅t+φ'0))=ddt(−A⋅ω⋅sin(ω⋅t+φ'0))=−A⋅ω2⋅cos(ω⋅t+φ'0)

Ecuación de aceleración

	Aceleración (cuando x → Seno )	Aceleración (cuando x → Coseno )
Con ω	$a = - A \cdot ω 2 \cdot sin (ω \cdot t + φ 0)$	$a = - A \cdot ω 2 \cdot cos (ω \cdot t + φ' 0)$
Con f	$a = - A \cdot (2 \cdot π \cdot f) 2 \cdot sin (2 \cdot π \cdot f \cdot t + φ 0)$	$a = - A \cdot (2 \cdot π \cdot f) 2 \cdot cos (2 \cdot π \cdot f \cdot t + φ' 0)$
Con T	$a = - A \cdot (2 \cdot π T) 2 \cdot sin (2 \cdot π T \cdot t + φ 0)$	$a = - A \cdot (2 \cdot π T) 2 \cdot cos (2 \cdot π T \cdot t + φ' 0)$

Para cualquier instante t se cumple que a(t)=a(t+T) .

Gráfica de aceleración a - t