Una partícula posee un movimiento armónico simple a lo largo de un eje X cuando su elongación x, o coordenada de posición sobre este eje, se expresa mediante una función sinusoidal del tiempo dado.
PERÍODO Y FRECUENCIA DEL M.A.S
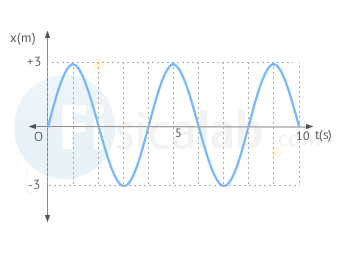
El período T del M.A.S es independiente de la amplitud y su fórmula es:
T= período ; f= frecuencia ; w= velocidad angular
Frecuencia
La frecuencia mide la cantidad de vueltas que se dan en un período de tiempo (normalmente un segundo). Se calcula con la siguiente fórmula:
La unidad más utilizada es el hertz que equivale a una vuelta en un segundo.
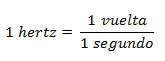
Período
El período mide el tiempo que se tarde en dar una vuelta completa y se mide en segundos. Es la inversa de la frecuencia.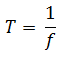
T = Período [s]
f = Frecuencia [Hz]
De esta forma, la frecuencia se puede calcular como la inversa del período.
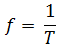
f = Frecuencia [Hz]
T = Período [s]
Posición
La posición de una partícula que sigue un movimiento armónico simple ( m.a.s.), también denominada elongación, viene determinada por la distancia x a la posición de equilibrio. Su unidad de medida en el Sistema Internacional es el metro (m). Se trata de una función sinusoidal (seno o coseno), que depende del tiempo x = f(t).
Ecuación de posición
| x → Seno | x → Coseno | |
| Con | ||
| Con f | ||
| Con T |
Donde:
- A: Amplitud máxima del movimiento. Representa la distancia máxima a la posición de equilibrio. Su unidad de medida en el Sistema Internacional es el metro (m)
- f: Frecuencia del movimiento. Es el número de oscilaciones o vibraciones que se producen en un segundo. Su unidad de medida en el Sistema Internacional es el Hertzio (Hz). 1 Hz = 1 oscilación / segundo = 1 s-1.
- T: Periodo del movimiento. El tiempo que tarda en cumplirse una oscilación completa. Es la inversa de la frecuencia T = 1/f . Su unidad de medida en el Sistema Internacional es el segundo (s).
ω : Frecuencia angular o pulsación. Representa el número de periodos comprendidos en 2·π segundos. Su unidad de medida en el sistema internacional es el radián por segundo ( rad/s ). Se encuentra relacionada con la frecuencia y el periodo del movimiento segúnω=2⋅πT=2⋅π⋅f φ0 yφ'0 : Fase inicial. Se trata del ángulo que representa el estado inicial de vibración, es decir, la posición x del cuerpo en el instante t = 0. Su valor depende de si has elegido un seno o un coseno para representar el movimiento.φ'0=φ0−π/2 Su unidad de medida en el Sistema Internacional es el radián (rad) .
Para cualquier instante t se cumple que x(t)=x(t+T) .
Gráfica de posición x - t

Velocidad
La velocidad instantánea determina la variación de posición que tiene el cuerpo en cada instante de tiempo t. Se define como la derivada de la posición respecto al tiempo.
Para obtener la expresión de la velocidad hemos de tener en cuenta que dependerá de si expresamos la posición como seno o como coseno:
v=ddt(A⋅sin(ω⋅t+φ0))=A⋅ω⋅cos(ω⋅t+φ0) v=ddt(A⋅cos(ω⋅t+φ'0))=−A⋅ω⋅sin(ω⋅t+φ'0)
Ecuación de velocidad
Velocidad
(cuando x → Seno ) | Velocidad (cuando x → Coseno ) | |
| Con | ||
| Con f | ||
| Con T |
Para cualquier instante t se cumple que v(t)=v(t+T) .
Gráfica de velocidad v - t

Aceleración
La aceleración instantánea determina la variación de velocidad que tiene el cuerpo en cada instante de tiempo t. Se define como la derivada de la velocidad respecto al tiempo.
Para obtener la expresión de la aceleración hemos de tener en cuenta que dependerá de si expresamos la posición como seno o como coseno:
a=d2dt2(A⋅sin(ω⋅t+φ0))=ddt(A⋅ω⋅cos(ω⋅t+φ0))=−A⋅ω2⋅sin(ω⋅t+φ0) a=d2dt2(A⋅cos(ω⋅t+φ'0))=ddt(−A⋅ω⋅sin(ω⋅t+φ'0))=−A⋅ω2⋅cos(ω⋅t+φ'0)
Ecuación de aceleración
| Aceleración (cuando x → Seno ) | Aceleración (cuando x → Coseno ) | |
| Con | ||
| Con f | ||
| Con T |
Para cualquier instante t se cumple que a(t)=a(t+T) .
Gráfica de aceleración a - t

No hay comentarios:
Publicar un comentario